Question

Find an equation of the line. Write the equation using function notation through left parenthesis 4 comma negative 4 right parenthesis​; perpendicular to 7y=x-14

Answer 1

The question is:

Find an equation of the line. Write the equation using function notation through (4, -4)​; perpendicular to 7y = x - 14

Answer: The equation of the line is f(x) = -7x + 24

Explanation:

We are given a line: 7y = x - 14.

We need to find the slope, and that means we need to rewite the slope in the form y = mx + c. Where m is the slope of the line.

7y = x - 14

Divide both sides by 7

y = (1/7)x - 2

Comparing this with y = mx + c, we can see that the slope, m = 1/7

We want to write an equation that is perpendicular to the equation 7y = x - 14.

The slope of a line perpendicular to a slope m is -1/m.

We have a slope 1/7, a line perpendicular to it has slope -7/1.

Now, we use the point-slope form to find our equation:

`y_2 - y_1 = m(x_2 - x_1)`.

The points given is
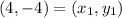`(4, -4) = (x_1, y_1)`. Substitute the values into the point-slope form equation.

y - (-4) = -7/1 (x - 4)

y + 4 = -7x + 28

The solution has to be in terms of y, so that we can write it using function notation.

Doing that,

y = -7x + 28 - 4

y = -7x + 24

To write it in function notation, simply put y = f(x)

so f(x) = -7x + 24.

Answer 2

The solution is in the attachment