Please find the file attached below (figure for the question)
To prove that area of the two triangles is equal we must know the formula for the area of a triangle and concept of concyclic points as given below:
Area of a Triangle:
Formula to find the area of a triangle is
Base can be any side of a triangle but height must be the side perpendicular to the base
Concyclic points:
Points which lie on the same circle having the same distance from the center of the circle.
Given Data:
Arc SO= Arc IM
chord SM= chord IO
Proof of Area of Triangle SOK=Area of Triangle IMK:
As the given points are concyclic points, so
Any of the above point is radius of the circle.
Thus,
Are of Triangle SOK:
where, SK is the Base for triangle SOK and OK is the Height for the triangle SOK
Area of Triangle IMK:
Where, KM is Base of the triangle IMK and IK is Height of the triangle IMK
As we know
SK=OK=KM=IM
We can say directly that area of both the triangles is same
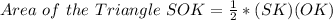 =
=
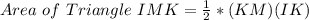
OR
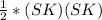
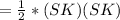
thus proved
Proof of SM=IO:
As points are concyclic so they all have same distance from the center of the circle
i.e.SK=OK=KM=IM
thus SM=IO