Question

At a certain time of the day, a tree that is x meters tall casts a shadow that is x-49 meters long. If the distance from the top of the tree to the end of the shadow is x+1 meters, what is the height , x of the tree ?

Answer 1

The height of the tree is 60 meters.

Step-by-step explanation:

Let the height of the tree be x. The tree casts a shadow of
`x-49` meters and the distance from the top of the tree to the end of the shadow is
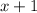`x+1` meters.

The sides of the triangle are attached in the image below:

Using pythagoras theorem,

`x^(2)+(x-49)^(2)=(x+1)^(2)`

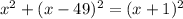
Expanding, we get,

`2 x^(2)-98 x+2401=x^(2)+2 x+1`

`2 x^(2)-98 x+2400=x^(2)+2 x`

`2 x^(2)-100 x+2400=x^(2)`

`x^(2)-100 x+2400=0`

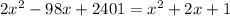
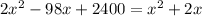
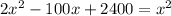
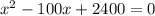
Solving the equation using the quadratic formula
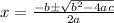`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`, we get,

`x=\frac{-(-100)\pm\sqrt{(-100)^(2)-4 \cdot 1 \cdot 2400}}{2 \cdot 1}`

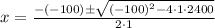
Simplifying, we have,

`x=(100\pm√(10000-9600))/(2)`

`x=(100\pm√(400))/(2)`

`x=\frac{100\pm{20}}{2}`

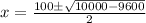
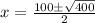
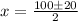
Thus,

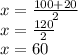`x=(100+20)/(2) \\x=(120)/(2) \\x=60` and
`x=(100-20)/(2) \\x=(80)/(2) \\x=40`

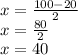
where the value
`x=40` is not possible because substituting the value
`x=40` in
`x-49` results in negative solution. Which is not possible.

Hence, the value of x is 60.

Thus, The height of the tree is 60 meters.