Question

Which is the simplified form of r Superscript negative 7 Baseline + s Superscript negative 12?

StartFraction 1 Over r Superscript 7 Baseline s Superscript 12 EndFraction
Negative r Superscript 7 Baseline minus s Superscript 12
StartFraction r Superscript 7 Over s Superscript 12 EndFraction
StartFraction 1 Over r Superscript 7 Baseline EndFraction + StartFraction 1 Over s Superscript 12 EndFraction
Mark

Answer 1

`\frac{1}{ {r}^(7) } + \frac{1}{ {s}^(12) }`

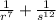
Explanation:

We want to simplify:

`{r}^( - 7) + {s}^( - 12)`

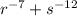
Let us rewrite as positive index to get:

`{r}^( - 7) + {s}^( - 12) = \frac{1}{ {r}^(7) } + \frac{1}{ {s}^(12) }`

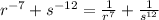
We now find LCM to get:

`{r}^( - 7) + {s}^( - 12) = \frac{ {r}^(7) + {s}^(12) }{ {r}^(7) {s}^(12) }`

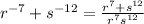
Therefore the simplified form of the given expresion is:

`\frac{ {r}^(7) + {s}^(12) }{ {r}^(7) {s}^(12) }`

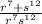
But from the provide option, they only want us to rewrite as positive index without simplifying further