Answer: Restating the Frequency distribution clearly
Class Frequency
2 up to 4 32
4 up to 6 48
6 up to 8 92
8 up to 10 32
a. Population mean (μ) = 6.22
b. Population Variance = 3.88
c. Standard deviation = 1.97
Explanation:
1. To solve this, we first of all have to form a frequency table, and in order to get the different components of the table, we have to state the formula of the most complex part of the question that is the standard deviation
Standard deviation (S) =√ [∑f(m-μ)² / ∑f - 1].
2. next, we will form the frequency table as shown below making sure to include all the components of the standard deviation formula.
Class f m f×m μ (m-μ) (m-μ)² f(m-μ)²
2-4 32 3 96 6.22 -3.22 10.3684 331.7888
4-6 48 5 240 6.22 -1.22 1.4884 71.4432
6-8 92 7 644 6.22 1.22 1.4884 136.9328
8-10 32 9 288 6.22 2.78 7.7284 247.3088
204 1268 787.4736
where:
f = frequency
m = midpoint
μ = mean
3. After getting f, and m, we can calculate the mean which is also known as the average value, as shown below:
mean (μ) : ∑(f × m) / ∑f Note that the symbol "∑" stands for "sum of"
∴ μ =
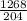 = 6.2157
= 6.2157
Rounding to 2 decimal places μ = 6.22
4. Next let us define what standard deviation is; the standard deviation is the extent to which a value differ from the mean value. The formula is shown below.
Standard deviation (S) =√ [∑f(m-μ)² / ∑f - 1]
S
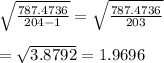
∴ S = 1.97 (to 2 decimal places)
5. finally, the variance is the square of the standard deviation and it is shown thus:
Variance (S²) =
 = 3.88 (2 decimal places).
= 3.88 (2 decimal places).