Question

A coincoin sold for ​$264 in 1977 and was sold again in 1989 for $475. Assume that the growth in the value V of the​ collector's item was exponential. Find the value k of the exponential growth rate. Assume Vo=264.

Answer 1

The exponential growth rate=k=0.0489

Step-by-step explanation:

The formula we are going to use is:

`V=V_oe^(kt)`

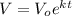
Where:

V is the final value

V_o is the initial value

K is the exponential growth

t is the time

In our case:

V=475

V_o=264

t=12 years

Required:

The exponential growth rate=k=?

Solution:

`475=264e^(k*12)\\k=(1)/(12)ln((475)/(264))\\ k=0.0489`

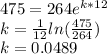
The exponential growth rate=k=0.0489