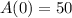Answer:
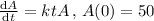
Explanation:
A(t) denotes the amount of oil in the barrel at time t.
As the amount of oil is decreasing at a rate proportional to the product of the time elapsed and the amount of oil present in the barrel,

Here, k is a constant term.
As a 100-gallon barrel initially contains half-full of oil,