Question

A loan processing office receives 4 loan requests every hour. The office has 2 departments. It takes the first department on average 20 minutes to do a preliminary check on the requests and 20% are rejected directly without going into the second department. The remaining 80% go into the second department and take 60 minutes per request and then either an acceptance or rejection letter is sent to the client. On average how many requests are in the first department (including those who are waiting)

Answer 1

On average how many requests are in the first department (including those who are waiting) is 1.32.

Explanation:

In this case, use the Little's law of queuing theory.

The Little's law states that the average number of customers in a fixed system (L) is equal to the average effective arrival rate (λ) multiplied by the average time a customer spends in the system (W).

The number of requests per hour in the 1st department is, λ₁ = 4.

It is provided that 20% are rejected directly by the 1st department without going into the 2nd department.

Then the number of requests per hour is, λ₂ =
`4* 80\%=4*0.80=3.2`

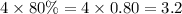
The average time a customer spends in the 1st department,

W₁ = 20 minutes = 0.33 hours.

The average time a customer spends in the 1st department,

W₂ = 60 minutes = 1 hour

On average how many requests are in the first department (including those who are waiting) is:

L = λ₁ × W₁

= 4 × 0.33

= 1.32

Thus, on average how many requests are in the first department (including those who are waiting) is 1.32.