Question

A family plans to have 3 children. For each birth, assume that the probability of a boy is the same as the probability of a girl. What is the probability that they will have at least one boy and at least one girl?

a.0.5
b.0.125
c.0.75
d.0.875

Answer 1

C. 0.75

Explanation:

Total Possible 8 Outcomes : GGG, BGG, GBG, GGB ,BBB, GBB, BGB, BBG

Probability of having atleast one boy & atleast one girl = 1- (Probability of having all girls, all boys)

Pr (All girls, All boys) = GGG, BBB = 2 outcomes

So, Pr [Atleast one boy & ateast one girl] = 1 - 2/8

= 6/8

= 0.75

Answer 2

(c), 0.75

Explanation:

It is given that, the probability of boy is same as the probability of girl.

Number of children family plans to have = 3

Consider, B be the event that represents that child is a boy

G be the event that represents that child is a girl.

The simple events for the provided case could be written as:

S = {(GGG, BBB, GBB, BGB, BBG, BBG, GBG, GGB)}

From above simple event, it is clear that

P(3 boys) = 1/8 and P(3 Girls) = 1/8

Thus, the probability of having at least one boy and at least one girl can be calculated as:

`Probability = 1- ((1)/(8) + (1)/(8) ) = (6)/(8) =(3)/(4)`

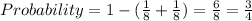
Thus, the required probability is 0.75.

Hence, the correct option is (c), 0.75