Question

A certain brand of tires of automobile tires has a mean life spanof 35,000 miles and a standard deviation of 2250 miles. (Assume thelife spans of the tires have a bell-shaped distribution.)

(a) The life spans of the three randomly selected tires are 34,000miles, 37,000 miles, and 31,000 miles. Find the z-score thatcorresponds to each life span. According to the z-scores, would thelife span of any of these tires be considered unusual?

(b) The life span of three randomly selected tires are 30,500miles, 37,250 miles, and 35,000 miles. Using the Empirical Rule,find the percentile that corresponds to each life span.

For part A I understand how to find the z-scores by using theequation: Z = X - μ / σ

34,000 miles z-score = -.44
37,000 miles z-score = .88
31,000 miles z-score = -1.77

If any of the z-scores are wrong please let me know and I alsounderstand whether or not the scores are considered unusual. Forthis care the scores are not considered unusual because they fallbetween -2 and 2.

I needed help for part B, I don't know where to begin withfinding the percentiles.

Answer 1

Part a : All the 3 z scores calculated in the question are accurate. Also as the values lie between -2 and 2 thus these z scores are not considered unusual.

Part b: The value 30500 is at 2.5% percentile, the value 37250 is at 84% percentile and the value 35000 is at 50% percentile.

Step-by-step explanation:

Part a:

All the 3 z scores calculated in the question are accurate. Also as the values lie between -2 and 2 thus these z scores are not considered unusual.

Part b:

For 30500

As the μ=35000 and σ=2250. Now calculating the value of 30500 in terms of μ and σ, so

`30500=35000-2(2250)=\mu-2\sigma`

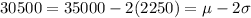
The value is given by μ-2σ.

The empirical rule indicates that 95% of all data values are within 2 standard

deviations of the mean and thus 100% — 95% = 5% of all data values are either more than or less than 2 standard deviations from the mean.

Since the normal distribution (bell-shaped distribution) is symmetric, 5%/2 =

2.5% of all data values are then more than two standard deviations below

the mean (while the other 2.5% of all data values are more than two standard

deviations above the mean).

This indicates that the value 30500 is at 2.5% percentile.

For 37250

As the μ=35000 and σ=2250. Now calculating the value of 37250 in terms of μ and σ, so

`37250=35000+2250=\mu +\sigma`

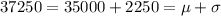
The value is given by μ+σ.

The empirical rule indicates that 68% of all data values are within 1 standard

deviations of the mean and thus 100% — 68% = 32% of all data values are either more than or less than 2 standard deviations from the mean.

Since the normal distribution (bell-shaped distribution) is symmetric, 32%/2 =16% of all data values are then more than two standard deviations below

the mean (while the other 16% of all data values are more than two standard

deviations above the mean).

In total, 16% + 68% = 84% of all data values is then below one standard

deviation below the mean, which corresponds with the 84th percentile.

This indicates that the value 37250 is at 84% percentile.

For 35000

As the μ=35000 and σ=2250. Now calculating the value of 35000 in terms of μ and σ, so

`35000=35000-0(2250)=\mu`

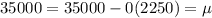
The value is given by μ.

The empirical rule indicates that 50% of all data values are less than the mean in a symmetric distribution and as the distribution is symmetric, thus This indicates that the value 35000 is at 50% percentile.