Question

A helicopter is flying horizontally at 8.15 m/s and an altitude of 18.5 m when a package of emergency medical supplies is ejected horizontally backward with a speed of 10.4 m/s relative to the helicopter. Ignoring air resistance, what is the horizontal distance between the package and the helicopter when the package hits the ground?

Answer 1

`d=39.27m`

Step-by-step explanation:

Let +y is upward direction and backward be +x direction

then we have given data

`v_(hg)=-8.15m/s\\v_(ph)=10.4m/s\\\\then\\v_(pg)=v_(hg)+v_(ph)\\v_(pg)=-8.15m/s+10.4m/s\\v_(pg)=2.25m/s`

From equation simple motion we find the time

So

`y_(f)=y_(i)+v_(yi)t+(1/2)a_(y) t^(2) \\ 0=18.5m+0+(1/2)(-9.8m/s^(2) )t^(2)\\-18.5=-4.9t^(2)\\t=3.7755s`

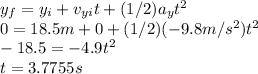
To get the distance between the point the package ejected to the point it the ground.

`v_(x)=x_(p)/t\\ x_(p)=v_(x)*t\\x_(p)=(2.25m/s)*(3.7755s)\\x_(p)=8.5m(backward)`

Now we have to get the distance the helicopter travels during same interval

`x_(h)=v_(hg)*t\\x_(h)=-8.15m/s*3.7755s\\x_(h)=30.77m(forward)`

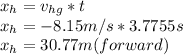
Now to get the distance between the package and helicopter when package hit the ground

`d=x_(p)-x_(h)\\d=8.5m-(-30.77m)\\d=39.27m`