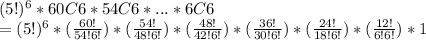Question

60 wedding guests are to be seated at 10 circular tables, each with 6 seats. Two seating arrangements are considered the same if the person to the left of each person is unchanged. How many seating arrangements are possible, and why? It is ok to leave your answer with factorials in it.

Answer 1

Explanation:

60 guests are there with 10 circular tables of 6 seats each.

First we have to select 6 persons from 60 for I table and next 6 persons for II table etc.

i.e.first table can be assigned 6 people in 60C6 ways

II table from remaining 54 in 54C6 ways

....

Each table with 6 persons can be arranged in a circular table in 5! ways

(since Two seating arrangements are considered the same if the person to the left of each person is unchanged)

Thus no of ways of allotting persons to different tables

= 60C6*54C6*48C6*42C6...*6C6

Each table allotment is in (6-1)! = 5! ways

Total ways of seating arrangement =
`(5!)^6 *60C6*54C6*...*6C6\\= (5!)^6 *((60!)/(54!6!) )*((54!)/(48!6!) )*((48!)/(42!6!) )*((36!)/(30!6!) )*((24!)/(18!6!) )*((12!)/(6!6!) )*1`