Answer:
$712.
Explanation:
We have been given that a fund earns a nominal rate of interest of 6% compounded every two years. We are asked to find the amount that must be contributed now to have 1000 at the end of six years.
We will use compound interest formula to solve our given problem.
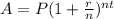 , where,
, where,
A = Final amount,
P = Principal amount,
r = Annual interest rate in decimal form,
n = Number of times interest is compounded per year,
t = Time in years.
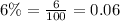
Since interest is compounded each two years, so number of compounding per year would be 1/2 or 0.5.
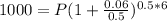
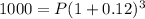
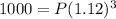

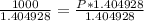
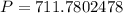
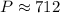
Therefore, an amount of $712 must be contributed now to have 1000 at the end of six years.