Question

A small truck is to be driven down a 4% grade at 70 mi/h. The coefficient of road adhesion is 0.95, and it is known that the braking efficiency is 80% when the truck is empty and decreases by one percentage point for every 100 lb of cargo added. Ignoring aerodynamic resistance, if the driver wants the truck to be able to achieve a minimum theoretical stopping distance of 275 ft from the point of brake application, what is the maximum amount of cargo (in pounds) that can be carried?

Answer 1

Maximum amount of cargo(in lbs) = 1455 lbs

Step-by-step explanation:

Assume the maximum amount of cargo is w ,

The breaking efficiency will be given by

1. E = (80 - 0.01 w) %

Stopping distance is given by formula ,

Stopping distance =
`(v^(2) )/(2g(u - 0.01n)E)`

where,

v (velocity), u (coefficient of road adhesion), n (grade)

Put E from equation 1

Stopping distance =
`(v^(2) )/(2g(u - 0.01n)(80 - 0.01w)0.01)`

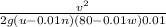
Stopping distance is given as 275 ft ,

V= 70 mi/hr = 70 x 1.4667 ft/s = 102.67 ft/s

Put all given values in above equation

275 =
`((102.67)^(2) )/(2(32.18)(0.95 - 0.01(4))(80 - 0.01w)0.01)`

(80 - 0.01w ) =
`((102.67)^(2) )/(2(32.18)(0.91)(0.01)(275))`

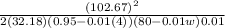
( 80 - 0.01w ) = 65.45

0.01w = ( 80 - 65.45)

w = 14.55 x 100

w = 1455 lbs