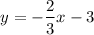Question

Find the equation of the line shown below

Answer 1

y = -x + 3

Explanation:

Slope = rise/run

Select 2 coordinate points. I'll do (-4,1) and (0,-3). The slope will be (-3-1)/(0-(-4)) = -4/4 = -1.

Plug that into the equation of a line, y-y1 = m(x-x1), where m is the slope.

y-1 = -1(x+4)

y-1 = -m - 4

y = -x + 3

Answer 2

This equation is in the slope-intercept form
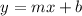`$y=m x+b$`, where the slope
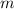`$m$` is approximately and the y-intercept b is -3 . The negative slope indicates that the line is decreasing as x increases, which matches the downward trend we see in the graph.

The line in the graph appears to cross the y-axis (where x=0) at a point that can be estimated visually.

Likewise, we can estimate the slope of the line by determining how much the line rises or falls over a given distance along the x-axis.

To find the equation of the line, we typically use the slope-intercept form of a line's equation, which is y = mx + b, where m is the slope of the line and b is the y-intercept.

The slope (m) of a line is calculated by the change in y over the change in x between two points (rise over run). The y-intercept (b) is the value of y where the line crosses the y-axis.

From the graph, we need to identify two clear points that the line passes through. It seems there is one point at the y-intercept and another point further along the line that we can use to calculate the slope.

Once we have these two points, we can calculate the slope and write the equation.

Let's identify these points and calculate the equation.

The equation of the line, estimated from the two points identified in the graph, is
`$y=-(2)/(3) x-3$`