Question

An equal-tangent sag vertical curve (with a negative initial and a positive final grade) is designed for 55 mi/h. The PVI is at station 240 + 00 and elevation 122 ft. The PVT is at station 242 + 30 and elevation 127.75 ft. What is the station and elevation of the lowest point on the curve?

Answer 1

The lowest point of the curve is at 239+42.5 ft where elevation is 124.16 ft.

Step-by-step explanation:

Length of curve is given as

`L=2(PVT-PVI)\\L=2(242+30-240+00)\\L=2(230)\\L=460 ft`

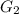`G_2` is given as

`G_2=(E_(PVT)-E_(PVI))/(0.5L)\\G_2=(127.5-122)/(0.5*460)\\G_2=0.025=2.5 \%`

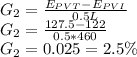
The K value is given from the table 3.3 for 55 mi/hr is 115. So the value of A is given as

`A=(L)/(K)\\A=(460)/(115)\\A=4`

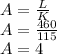
A is given as

`-G_1=A-G_2\\-G_1=4.0-2.5\\-G_1=1.5\\G_1=-1.5\%`

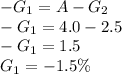
With initial grade, the elevation of PVC is

`E_(PVC)=E_(PVI)+G_1(L/2)\\E_(PVC)=122+1.5%(460/2)\\E_(PVC)=125.45 ft\\`

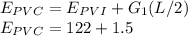
The station is given as

`St_(PVC)=St_(PVI)-(L/2)\\St_(PVC)=24000-(230)\\St_(PVC)=237+70\\`

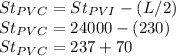
Low point is given as

`x=K * |G_1|\\x=115 * 1.5\\x=172.5 ft`

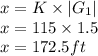
The station of low point is given as

`St_(low)=St_(PVC)-(x)\\St_(low)=23770+(172.5)\\St_(low)=239+42.5 ft\\`

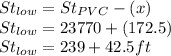
The elevation is given as

`E_(low)=(G_2-G_1)/(2L) x^2+G_1x+E_(PVC)\\E_(low)=(2.5-(-1.5))/(2*460) (1.72)^2+(-1.5)*(1.72)+125.45\\E_(low)=124.16 ft`

So the lowest point of the curve is at 239+42.5 ft where elevation is 124.16 ft.