Answer:
Pr(N < 4.2) = 0.295
Step-by-step explanation:
given data
flow rate q = 300 veh/h
reaction time = 2.5 s
oncoming vehicle to stop = 1.7 s
solution
we know here that ongoing vehicle head way between successive vehicles is here greater than (1.5 + 2.5) = 4.2 second
so that driver pulling out will not be in an accident
and if head way is less than 4.2 seconds then driver pulling out will be accident
here q is 300 vehicles/hour,
then λ= 0.0833 vehicles/second
than probability will be
Pr(N < 4.2) = 1 -
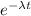 ................ 1
................ 1
put here value
Pr(N < 4.2) = 1 -
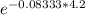
Pr(N < 4.2) = 0.295