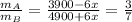Answer:
210 grams
Explanation:
Simply, the final amount of each container will not be changed because we add and subtract same amount of solution in the end. Therefore final mass of Container A is 300 grams and final mass of Container B is 700 grams.
However if concentration of the both containers is the same, final amont of the salt should have following relation;
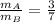
where
 is the amount of salt in container A, and
is the amount of salt in container A, and
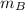 is the amount of salt in container B.
is the amount of salt in container B.
Suppose that the x is the amount that we take away from both containers and than pour into other container. For container A, finally we will have (300-x) grams with 13% concentration and x grams with 7% concentration and vice versa. Total amount of salt in container can be written as,
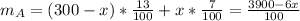
similarly for container B ,
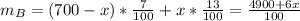
if we replace these values in first equation above and solve for the x,