Question

Solve the system using either Gaussian elimination with back-substitution or Gauss-Jordan elimination. (If there is no solution, enter NO SOLUTION. If the system has an infinite number of solutions, set y = t and solve for x in terms of t.) −3x + 5y = −34 3x + 4y = −11 4x − 8y = 52

Answer 1

The solution of the system of equations is
`x=3\\y=-5`.

Explanation:

Gauss–Jordan elimination is a procedure for converting a matrix to reduced row echelon form using elementary row operations.

It relies upon three elementary row operations one can use on a matrix:

1. Swap the positions of two of the rows
2. Multiply one of the rows by a nonzero scalar.
3. Add or subtract the scalar multiple of one row to another row.

To find the solution of the system

`-3x + 5y = -34 \\3x + 4y = -11 \\4x -8y = 52`

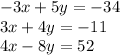
using Gauss-Jordan elimination you must:

Step 1: Transform the augmented matrix to the reduced row echelon form.

In an augmented matrix, each row represents one equation in the system and each column represents a variable or the constant terms.

This is the augmented matrix that represents the system.

`\left[ \begin{array}{ccc} -3 & 5 & -34 \\\\ 3 & 4 & -11 \\\\ 4 & -8 & 52 \end{array} \right]`

Using elementary matrix operations, we get that

Row Operation 1: Add row 1 to row 2
`\left(R_2=R_2+R_1\right)`

Row Operation 2: Divide row 1 by −3
`\left(R_1=(R_1)/(-3)\right)`

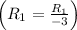
Row Operation 3: Subtract row 1 multiplied by 4 from row 3
`\left(R_3=R_3-\left(4\right)R_1\right)`

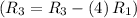
Row Operation 4: Divide row 2 by 9
`\left(R_2=(R_2)/(9)\right)`

Row Operation 5: Add row 2 multiplied by 5/3 to row 1
`\left(R_1=R_1+\left((5)/(3)\right)R_2\right)`

Row Operation 6: Add row 2 multiplied by 4/3 to row 3
`\left(R_3=R_3+\left((4)/(3)\right)R_2\right)`

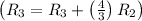
This is the reduced row echelon form matrix

`\left[ \begin{array}{ccc} 1 & 0 & 3 \\\\ 0 & 1 & -5 \\\\ 0 & 0 & 0 \end{array} \right]`

Step 2: Interpret the reduced row echelon form

The reduced row echelon form of the augmented matrix corresponds to the system

`x=3\\y=-5`