Question

Consider the famous Gamma function, defined by Γ(x) = R [infinity] 0 t x−1 e −t dt. Using mathematical induction, prove that Γ(n + 1) = n! for any n ∈ N ∪ {0}, where n! = n(n − 1)· · · 3 · 2 · 1 is the usual factorial function

Answer 1

See proof below

Explanation:

The inductive proof consists on the following steps:

1) Base case: for n=0, we will prove that Γ(1)=0!=1. We have that

`\gamma(1)=\int_(0)^(\infty)t^(1-1)e^(-t)dt=\int_(0)^(\infty)t^(1-1)e^(-t)dt`

`=-e^(-t)|^(\infty)_(0)=0+e^(0)=1`

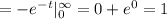
Hence the base case holds.

2) Inductive step: suppose that Γ(n + 1) = n! for some natural number n. We will prove that Γ((n + 1)+1) = (n+1)!

`\gamma(n+2)=\int_(0)^(\infty)t^(n+2-1)e^(-t)dt=\int_(0)^(\infty)t^(n+1)e^(-t)dt`

Use integration by parts, with the following parts:

u=t^{n+1}, du=(n+1)t^n

dv=e^{-t}, v=-e^{-t}

`\gamma(n+2)=-e^(-t)t^(n+1)|^(\infty)_(0)+(n+1)\int_(0)^(\infty)t^(n)e^(-t)dt`

`=(n+1)\gamma(n+1)=(n+1)n!=(n+1)!`

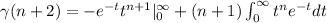
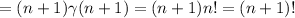
and we used the induction hypotheses on this last line. Also, -t^n e^-t tends to zero as n tends to infiity (the exponential decays faster than any polynomial).

We have proved the statement for n+1, and by mathematical induction, the statement holds for all n.