Question

Water is being boiled in an open kettle that has a 0.52-cm-thick circular aluminum bottom with a radius of 12.0 cm. If the water boils away at a rate of 0.409 kg/min, what is the temperature of the lower surface of the bottom of the kettle? Assume that the top surface of the bottom of the kettle is at 100.0∘C.

Answer 1

`T_b=107.3784\ ^(\circ)C`

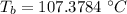
Step-by-step explanation:

Given:

• thickness of the base of the kettle,
  `dx=0.52\ cm=5.2* 10^(-3)\ m`

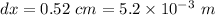
• radius of the base of the kettle,
  `r=0.12\ m`

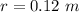
• temperature of the top surface of the kettle base,
  `T_t=100^(\circ)C`

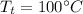
• rate of heat transfer through the kettle to boil water,
  `\dot Q=0.409\ kg.min^(-1)`

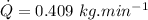
• We have the latent heat vaporization of water,
  `L=2260* 10^3\ J.kg^(-1)`

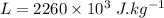
• and thermal conductivity of aluminium,
  `k=240\ W.m^(-1).K^(-1)`

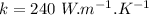
So, the heat rate:

`\dot Q=(0.409* 2260000)/(60)`

`\dot Q=15405.67\ W`

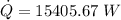
From the Fourier's law of conduction we have:

`\dot Q=k.A.(dT)/(dx)`

`\dot Q=k* \pi.r^2* (T_b-T_t)/(5.2* 10^(-3))`

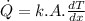
where:

`A=` area of the surface through which conduction occurs

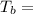`T_b=` temperature of the bottom surface

`15405.67=240* \pi* 0.12^2* (T_b-100)/(5.2* 10^(-3))`

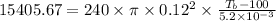
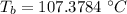`T_b=107.3784\ ^(\circ)C` is the temperature of the bottom of the base surface of the kettle.