Answer:
0.007773% probability that he would have done at least this well if he had no ESP.
Explanation:
For each coin flip, there are only two possible outcomes. Either the man gets the answer right, or he does not. The probabilities for each coin toss are independent, so we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
He gets 22 out of 25 correct. What is the probability that he would have done at least this well if he had no ESP?
If he had no ESP, the probability of getting each flip right is
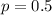 , since tails and heads are equally as likely.
, since tails and heads are equally as likely.
There are 25 throws, so

This probability is
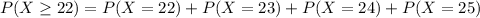
In which
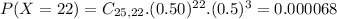
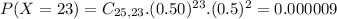
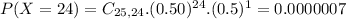
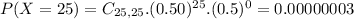
So
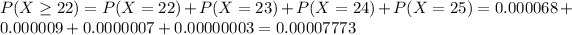
0.007773% probability that he would have done at least this well if he had no ESP.