Question

Consider the endothermic reactions in Exercise 2-50. Let A denote the event that a reaction's final temperature is 271 K orless. Let B denote the event that the heat absorbed is above target. Determine the following probabilities.(a) P(A n B) (b) P(A u B) (c) P(A’u 3')((1) Use the total probability rule to determine P(A)2-50. The following table summarizes 204 endothermic reac-tions involving sodium bicarbonate.Final TemperatureConditions Heat Absorbed (cal)Below Target Above Target266 K 12 40271 K 44 16274 K 56 36Let A denote the event that a reaction’s final temperature is 271 Kor less. Let B denote the event that the heat absorbed is belowtarget. Determine the number of reactions in each of thefollowing events.(a) AnB (b) A’ (c) AUB (d) AUB’ (e) A’nB’

Answer 1

Explanation:

Hello!

Using the information data of 204 endotermic reactions, two events were determined:

A: "the reactions final temperature is 271K or less"

B: "the heat absorbed is above target"

a) P(A∩B) is the intersection between the two events, this means, all the exotermic reaction with final temperature of 271K and less and absorved heat above target:

P(A∩B)=
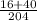`(16+40)/(204)`= 0.274

b)P(A∪B) is the probability that the reactions had a final temperature of 271K or are above target, the events A and B are not mutually exclusive, since both can occur at the same time (their intersection isn't void), so you calculate the probability as:

P(A∪B)= P(A) + P(B) - P(A∩B)

To calculate the probability of event A, you have to divide the number of reactions whose final temperature or less by the total number of endotermic reactions, symbolically:

`P(A)= (44+16+12+40)/(204)= 0.549`

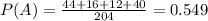
The probability of event B is the quotient between all reactions above target and the total of reactions, symbolically:

`P(B)= (40+16+36)/(204) = 0.451`

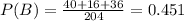
Then

P(A∪B)= 0.549 + 0.451 - 0.274= 0.726

c) P(A'∪B')

P(A'∪B')= P(A') + P(B') - P(A'∩B')

If A' is the complementary event of A, meaning all endotermic reactions above a final temperature of 271K, then it's probability is:

P(A')= 1 - P(A)= 1 - 0.549= 0.451

And B' the complementary event of B, this includes all reactions with heat absortion below target, it's probability is:

P(B')= 1 - P(B)= 1 - 0.451= 0.549

And the intersection between both events is:

P(A'∩B')= 56/204= 0.274

Then

P(A'∪B')=0.451 + 0.549 - 0.274= 0.726

I hope it helps!