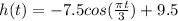Question

A Ferris wheel is 25 meters in diameter and boarded from a platform that is 1 meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 10 minutes. The function h(t) gives a person’s height in meters above the ground t minutes after the wheel begins to turn.

Part I: Complete the following steps:

Find the amplitude, midline, and period of h(t).
Find the domain and range of the function h(t) and
Find a formula for the height function h(t).

Answer 1

Amplitude = 9.5

Midline = 7.5

Period =
`(\pi )/(3)`

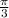
Explanation:

Thinking process:

The question is a sinusoidal variation since there is a linear distance in the vertical as something that is revolving.

The minimum height is 1 meter. The diameter of the wheel is 25 meters

From the plot, we know that he maximum height is 18 meters and the middle is 9.5 meters, meaning that the height varies by 7.5 meters.

The minimum height is at time t = 0, the maximum height when the wheel is gone 1/2 around. This takes place at t = 5 minutes, and the minimum height is again reached in 10 minutes.

By interpolation, this gives:

`h(t) = -7.5cos((\pi t)/(3) ) + 9.5`