Question

How many different 4-digit personal identification numbers are possible if no digit can be used twice?

Answer 1

The answer on Edge is B, or 5040.

If numbers range from 0-9 that means you start with 10 possible digits.

So: 10 x 9 x 8 x 7 = 5040.

Answer 2

560

Explanation:

We have 10 digits:

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

For the first place we have 10 digits to choose from.

For the second place we have 9 digits to choose from (one has already been chosen)

For the third 8 digits, and for the last 7.

Total 4-digit personal identification numbers is equal:

10 · 9 · 8 · 7 = 560

You can use the variations without repetition:

`V^k_n=(n!)/((n-k)!)`

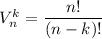
Variation is a way of selecting k items from a collection of n items (k ≤ n), such that the order of selection does matter. The repetition of items is not allowed.

We have

n = 10, k = 4

Substitute:

`V^(4)_(10)=(10!)/((10-4)!)=(6!\cdot7\cdot8\cdot9\cdot10)/(6!)=7\cdot8\cdot9\cdot10=560`