Answer:
36.66
Step-by-step explanation:
The mean of a discrete uniform distribution is the average of the boundaries:
μ=
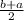
The variance of a discrete uniform distribution is the difference of the boundaries decreased by 1 and squared, decrease by 1 and divided by
σ^2=

a)
Given:
a = 620 nm
b = 640 nm
Use the formulas to determine the mean and variance:
μ=
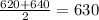
σ^2=

=(640-620+1)^2-1/12
=36.66