Question

1. An economy has three sectors producing products Product 1, Product 2, and Prod- uct 3. • To produce 1 unit of Product 1 requires 0.20 units of Product 1, 0.15 units of Product 2, and 0.10 units of Product 3. • To product 1 unit of Product 2 it takes 0.14 units of Product 1, 0.05 units of Product 2, and 0.12 units of Product 3. • To produce 1 unit of Product 3 it takes 0.14 units of Product 1, and 0.08 units of Product 2. (a) What should the total production be set at in order to satisfy an external de- mand of 100 units of Product 1, 120 units of Product 2, and 150 units of Product 3? (b) Individually interpret each entry in the third column of (I − M)−1.

Answer 1

Answer: Check the attached for the solution

Step-by-step explanation:

Answer 2

Part a: In order to meet the external demand of 100 units of Product 1, 120 units of Product 2 and 150 units of Product 3, the total production of 147.06 units of Product 1, 171.27 units of Product 2 and 184.29 units of Product 3 are to be produced.

Part b: The individual entry of 3rd column (I-M)^-1 signifies the role of the demand of 3rd product for total estimation of product 1, product 2 and product 3 respectively.

Step-by-step explanation:

The matrix form of the equation is given as

`\left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right] =\left[\begin{array}{ccc}0.02&.0.15&0.10\\0.14&0.05&0.12\\0.14&0.08&0\end{array}\right] \left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right] +\left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right] _(external)`

where

`\left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right] _(external)=\left[\begin{array}{c}100\\120\\150\end{array}\right]`

so the equation now becomes

`\left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right] =\left[\begin{array}{ccc}0.02&.0.15&0.10\\0.14&0.05&0.12\\0.14&0.08&0\end{array}\right] \left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right] +\left[\begin{array}{c}100\\120\\150\end{array}\right]`

From here it is given that

`P=MP+\Delta`

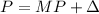
Or

`P-MP=\Delta\\P(I-M)=\Delta\\P=(I-M)^(-1)\Delta`

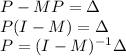
Here

`P=\left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right] \\M=\left[\begin{array}{ccc}0.02&.0.15&0.10\\0.14&0.05&0.12\\0.14&0.08&0\end{array}\right] \\\Delta=\left[\begin{array}{c}100\\120\\150\end{array}\right]`

So now I-M is given as

`\\I-M=\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right] -\left[\begin{array}{ccc}0.02&0.15&0.10\\0.14&0.05&0.12\\0.14&0.08&0\end{array}\right] \\ I-M=\left[\begin{array}{ccc}1-0.02&0-0.15&0-0.10\\0-0.14&1-0.05&0-0.12\\0-0.14&0-0.08&1-0\end{array}\right] \\I-M=\left[\begin{array}{ccc}0.98&-0.15&-0.10\\-0.14&0.95&-0.12\\-0.14&-0.08&1\end{array}\right]`

Now the inverse is calculated as

`(I-M)^(-1)=(1)/(det(I-M))Adj(I-M)`

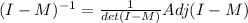
So the adjoint of (I-M) is calculated as

`adj(I-M)=adj(\left[\begin{array}{ccc}0.98&-0.15&-0.10\\-0.14&0.95&-0.12\\-0.14&-0.08&1\end{array}\right])\\adj(I-M)=\left[\begin{array}{ccc}0.9404&0.1580 & 0.1130\\0.1568&0.9660& 0.1316\\0.1442 &0.0994 & 0.9100\end{array}\right]\\`

Also the determinant is given as

`|I-M|=\left|\begin{array}{ccc}0.98&-0.15&-0.10\\-0.14&0.95&-0.12\\-0.14&-0.08&1\end{array}\right|\\|I-M|=0.8837`

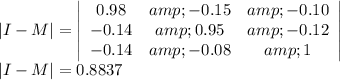
So the inverse is given as

`(I-M)^(-1)=(1)/(det(I-M))Adj(I-M)`

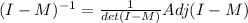
`(I-M)^(-1)=(1)/(0.8837)\left[\begin{array}{ccc}0.9404&0.1580 & 0.1130\\0.1568&0.9660& 0.1316\\0.1442 &0.0994 & 0.9100\end{array}\right]\\\\(I-M)^(-1)=\left[\begin{array}{ccc}1.0642 & 0.1788 & 0.1279\\ 0.1774 &1.0932 & 0.1489\\ 0.1632 & 0.1125 & 1.0298\end{array}\right]\\`

So the total demand of each product to meet the external demand is given as

`P=(I-M)^(-1)\Delta`

`\left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right]=\left[\begin{array}{ccc}1.0642 & 0.1788 & 0.1279\\ 0.1774 &1.0932 & 0.1489\\ 0.1632 & 0.1125 & 1.0298\end{array}\right]\left[\begin{array}{c}100\\120\\150\end{array}\right]\\\\\left[\begin{array}{c}P_1\\P_2\\P_3\end{array}\right]=\left[\begin{array}{c}147.06\\ 171.27 \\184.29\end{array}\right]\\`

So in order to meet the external demand of 100 units of Product 1, 120 units of Product 2 and 150 units of Product 3, the total production of 147.06 units of Product 1, 171.27 units of Product 2 and 184.29 units of Product 3 are to be produced.

Part b

The individual entry of 3rd column (I-M)^-1 signifies the role of the demand of 3rd product for total estimation of product 1, product 2 and product 3 respectively.