Answer:
70.94 mm is the upper control level with a 99.7% level of confidence.
Explanation:
We are given the following data:
69, 72, 71, 70, 68
Population mean = 70 mm
Population standard deviation = 1.25 mm
We have to find the upper control level with a 99.7% level of confidence.
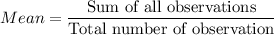
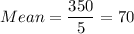
99.7% Confidence interval:
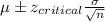
Putting the values, we get,
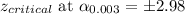
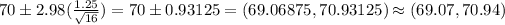
Thus, 70.94 mm is the upper control level with a 99.7% level of confidence.