Question

At equilibrium, the concentrations in this system were found to be [N2]=[O2]=0.300 M and [NO]=0.500 M.N2(g)+O2(g)−⇀↽−2NO(g)If more NOis added, bringing its concentration to 0.800 M, what will the final concentration of NO be after equilibrium is re‑established?

Answer 1

[NO] = 0.636 M

Step-by-step explanation:

The equation for the reaction = N₂(g) + O₂(g) ⇄ 2NO(g)

Given that [N₂]=[O₂]= 0.300 M and [NO]=0.500 M

The equilibrium constant
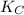`K_(C)` for the above equation can be written as:

`K_(C)= ([NO]^2)/([N_2][O_2])`

(since there are 2 moles of NO and 1 mole of N₂ and O₂ in the equation above).

`K_(C)= ([0.500]^2)/([0.300][0.300])`

`=(0.25)/(0.09)`

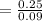
= 2.778

Furthermore, the question proceeds by stating that when more NO is added, there is increase in concentration, bringing it to 0.800 M.

Let construct an ICE table in order to determine the change in concentration

N₂(g) + O₂(g) ⇄ 2NO(g)

Initial (M) 0.300 0.300 0.800

Change (M) + x + x -2x

Equilibrium (M) 0.300+x 0.300+x 0.800-2x

Again,
`K_(C)= ([NO]^2)/([N_2][O_2])`

`2.778 = ([0.800-2x]^2)/([0.300+x][0.300+x])`

`2.778 = ([0.800-2x]^2)/([0.300+x]^2)`

Squaring both the Left-hand side(L.H.S) and the Right-hand side(R.H.S), we have:

`1.667=([0.800-2x])/([0.300+x])`

1.667[0.300+x] = [0.800-2x]

0.5001 + 1.667x = 0.800 - 2x

0.5001 - 0.800 = -1.667x - 2x

- 0.2999 = -3.667x

x =
`(-0.2999)/(-3.667)`

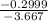
x = 0.082

So, the final concentration of NO from the ICE table after the equilibrium has been re-established is;

[NO] = 0.800 - 2x

[NO] = 0.800 - 2(0.082)

[NO] = 0.636 M

Therefore, the final concentration of NO be after equilibrium is re‑established = 0.636 M