The value of x is 1
Step-by-step explanation:
The equation is
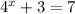
Subtracting both sides by 3, we get,
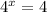
Taking log on both sides, we get,
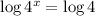
Rewriting the equation by
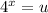
Thus, we have,
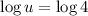
Applying log rule, if
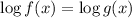 , then
, then
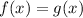
Thus,
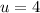
Substituting
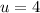 in
in
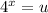 , we get,
, we get,
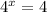
Also, since,
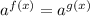 , then
, then
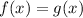
Thus,

Hence, the value of x is 1