Question

In 1980 the population of alligators in a particular region was estimated to be 1200. In 2007 the population had grown to an estimated 7500. Using the Malthusian law for population growth, estimate the alligator population in this region in the year 2020. The alligator population in this region in the year 2020 is estimated to be (Round to the nearest whole number as needed.)

Answer 1

The alligator population in this region in the year 2020 is estimated to be 18144

Explanation:

Malthus population model has the following format:

`P(t) = P(0)e^(rt)`

In which P(0) is the initial population and r is the growth rate.

In 1980 the population of alligators in a particular region was estimated to be 1200.

This means that
`P(0) = 1200`

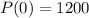
In 2007 the population had grown to an estimated 7500.

2007 is 27 years after 1980, because 2007-1980 = 27.

So

`P(27) = 7500`

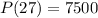
Replacing this into the equation, allows us to find the value of r.

`P(t) = P(0)e^(rt)`

`7500 = 1200e^(27r)`

`e^(27r) = (7500)/(1200)`

`e^(27r) = 6.25`

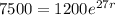
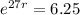
Applying ln to both sides, which is the inverse operation of the exponential

`\ln{e^(27r)} = ln(6.25)`

`27r = 1.8326`

`r = (1.8326)/(27)`

`r = 0.0679`

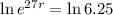
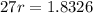
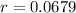
So

`P(t) = 1200e^(0.0679t)`

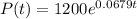
The alligator population in this region in the year 2020 is estimated to be

2020 - 1980 = 40

So this is P(40).

`P(t) = 1200e^(0.0679t)`

`P(40) = 1200e^(0.0679*40) = 18144`

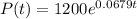
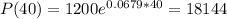
The alligator population in this region in the year 2020 is estimated to be 18144