Answer:
Obese people
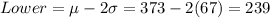

Lean People
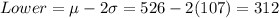
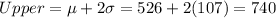
Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
The empirical rule, also referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution, "almost all data falls within three standard deviations (denoted by σ) of the mean (denoted by µ). Broken down, the empirical rule shows that 68% falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ)".
Solution to the problem
Obese people
Let X the random variable that represent the minutes of a population (obese people), and for this case we know the distribution for X is given by:
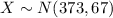
Where
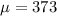 and
and
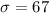
On this case we know that 95% of the data values are within two deviation from the mean using the 68-95-99.7 rule so then we can find the limits liek this:
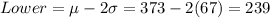

Lean People
Let X the random variable that represent the minutes of a population (lean people), and for this case we know the distribution for X is given by:
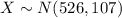
Where
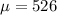 and
and
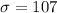
On this case we know that 95% of the data values are within two deviation from the mean using the 68-95-99.7 rule so then we can find the limits liek this:
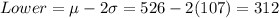
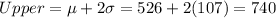
The interval for the lean people is significantly higher than the interval for the obese people.