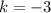Question

Given the function f(x) = x^2 and k = -3, which of the following represents a vertical shift?

Answer 1

The equation that represents the vertical shift is g(x) = x² - 3

How to determine which represents a vertical shift?

From the question, we have the following parameters that can be used in our computation:

f(x) = x²

Also, we have

k = -3

The function that represents the vertical shift is calculated as

g(x) = f(x) + k

Substitute the known values into the equation

g(x) = x² - 3

Hence, the expression that represents the vertical shift is g(x) = x² - 3

Question

Given the function f(x) = x^2 and k = -3, which of the following represents a vertical shift?

g(x) = (x + 3)²

g(x) = (x - 3)²

g(x) = x² + 3

g(x) = x² - 3

Answer 2

`k=-3` represents the vertical shift.

Step-by-step explanation:

It is given that the function
`f(x)=x^(2)` and
`k=-3`

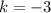
Now, we shall determine which of these two represents the vertical shift.

If the translated graph is shifted k units upward, then the translated function will be of the form
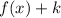`f(x)+k` where k shifts the k units upward.

Similarly, If the translated graph is shifted k units downward, then the translated function will be of the form
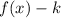`f(x)-k` where k shifts the k units downward.

Thus, the vertical shift of the function is represented by k units.

Hence,
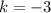`k=-3` represents the vertical shift.