Question

Find two numbers whose sum is -2 and whose difference is -6.

Answer 1

Explanation:

x+y=-2

x-y=-6

x=-2-y

(-2-y)-y=-6

-2-2y=-6

-2y=-4

y=2

x=-4

Answer 2

Answer: -4 and 2

Explanation:

Let the first number be x and the second number be y , then from the question:

`x + y = -2` ........................ equation 1

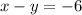`x - y = -6` ...................... equation 2

solving the of simultaneous linear equation by substitution method , make x the subject of the formula from equation 1 , that is

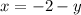`x = -2 - y` ................. equation 3

substitute
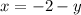`x = -2 - y` into equation 2 , then we have

`-2 - y - y = -6`

`-2 - 2y = -6`

`-2 + 6 = 2y`

`4 = 2y`

`y = 2`

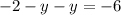
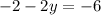
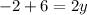
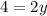
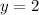
substitute
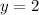`y = 2` into equation 3 to find the value of x , then we have

`x = -2 - 2`

`x = -4`

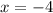
check:

`x + y = -2`

`-4 + 2 = -2`

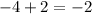
Also

`x - y = -6`

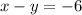
-4 - 2 = -6

Therefore: the numbers are -4 and 2