Answer:
smallest positive integer with 5 positive divisor is 16
smallest positive integer with 60 positive divisor is 5040
Explanation:
given data
precisely positive divisors = 5
precisely positive divisors = 60
solution
we take here
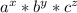 is express as
is express as
= (x+1) × (y+1) × (z+1)
so put here now x is 4
and z = y = 0 and a is least integer more than 1 it will be 2
and b and c ≥ 1
and
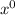 is = 1
is = 1
so
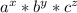 is
is
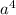 is =
is =
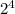 = 16
= 16
so smallest positive integer with 5 positive divisor is 16
and
same like 60 positive divisors
dn = ( a1+1 ) × ( a2+1 ) × ( a3+1 ) ............ ( an+1 )
n =
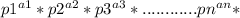
n = 7 × 5 × 3² ×
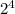
n = 5040
smallest positive integer with 60 positive divisor is 5040