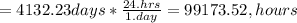Answer:
Part (a) The flow rate per unit width of the aquifer is 1.0875 m³/day
Part (b) The specific discharge of the flow is 0.0363 m/day
Part (c) The average linear velocity of the flow is 0.242 m/day
Part (d) The time taken for a tracer to travel the distance between the observation wells is 4132.23 days = 99173.52 hours
Step-by-step explanation:
Part (a) the flow rate per unit width of the aquifer
From Darcy's law;
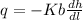
where;
q is the flow rate
K is the permeability or conductivity of the aquifer = 25 m/day
b is the aquifer thickness
dh is the change in th vertical hight = 50.9m - 52.35m = -1.45 m
dl is the change in the horizontal hight = 1000 m
q = -(25*30)*(-1.45/1000)
q = 1.0875 m³/day
Part (b) the specific discharge of the flow
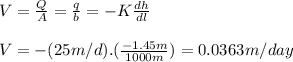
V = 0.0363 m/day
Part (c) the average linear velocity of the flow assuming steady unidirectional flow
Va = V/Φ
Φ is the porosity = 0.15
Va = 0.0363 / 0.15
Va = 0.242 m/day
Part (d) the time taken for a tracer to travel the distance between the observation wells
The distance between the two wells = 1000 m
average linear velocity = 0.242 m/day
Time = distance / speed
Time = (1000 m) / (0.242 m/day)
Time = 4132.23 days