Question

particle has a constant acceleration of 5.8 m/s2. (Due to the nature of this problem, do not use rounded intermediate values in your calculations—including answers submitted in WebAssign.) (a) If its initial velocity is 2.1 m/s, at what time (in s after t = 0) is its displacement 4.0 m? (No Response) 0.867 s (b) What is its speed at that time (in m/s)? (No Response) 7.13 m/s

Answer 1

a) t = 0.86 sec

b) v = 7.128 m/s

Step-by-step explanation:

Given data:

Constant acceleration = 5.8 m/s^2

Initial velocity = 2.1 m/s

Displacement = 4.0 m

kinematic equation is given as

`X -X_o = v_o * t + (1)/(2) at^2`

`X- X_o =  4.0 m`

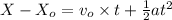
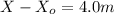
v = 2.1 m/s

a = 5.8 m/s^2

plugging all value in the above relation

`4 =  2.1t + (1)/(2) 5.8t^2`

`2.9t^2 + 2.1t - 4 = 0`

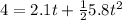
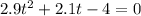
solve for t

`t = (-2 \pm √(2.1^2 -(4* 2.9 * (-4)))/(2* 2.9)`

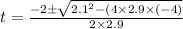
t = 0.86 sec

b) kinematic equation relating to velocity is given as

`v = v_0 + at`

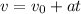
solving for velocity

`v = 2.1 + 5..8* 0.867`

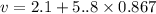
v = 7.128 m/s