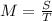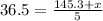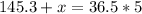Question

A 10-yr-old competes in gymnastics. For several competitions, she received the following "All-Around" scores: 35.5, 36.3. 36.6, and 36.9. Her coach recommends that gymnasts whose "All-Around" scores average at least 36.5 moves up to the next level. What "Ail-Around" scores in the next competition would result in the child being eligible to move up? The child needs a score of _____ to move up to the next level of the competition.

Answer 1

The child needs a score of 37.2 to move up to the next level of the competition.

Explanation:

The mean is the sum of all scores divided by the number of competions. So

`M = (S)/(T)`

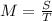
In which S is the sum of all her scores and T is the number of competitions.

The child has five competions:

Which means that
`T = 5`

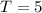
She has to get a mean of at least 36.5, so
`M = 36.5`

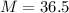
Her scores are: 35.5, 36.3. 36.6, and 36.9. Her last score, i am going to call x. So

`S = 35.5 + 36.3 + 36.6 + 36.9 + x = 145.3 + x`

The child needs a score of _____ to move up to the next level of the competition.

This score is x. So

`M = (S)/(T)`

`36.5 = (145.3 + x)/(5)`

`145.3 + x = 36.5*5`

`x = 37.2`