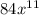The product of the expression is
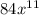
Step-by-step explanation:
The expression is
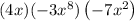
Let us simplify the expression by multiplying the first two terms.
Thus, we have,
![[(4 x)(-3 x ^8)]\left(-7 x^(2)\right)](https://img.qammunity.org/2021/formulas/mathematics/high-school/somlracsk0m4gj578k7iu45o35ugwcurgn.png)
First, multiplying the coefficients, we get,
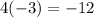
Since, the base x is common for both the terms, we can add the exponent.
Thus, we get,
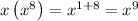
Thus, the simplification of the first two terms, we have,
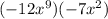
Similarly, we shall multiply the terms
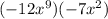 , we get,
, we get,
Multiplying the coefficients, we have,
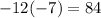
Adding the exponents, we have,
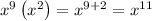
Thus, this gives
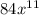
Hence, the product of the expression is