Question

Suppose the work required to stretch a spring from 1.1m beyond its natural length to a meters beyond its natural length is 5 J, and the work required to stretch the spring from a meters beyond its natural length to 4.8 m beyond its natural length is 9 J. Find the spring constant k and the value of a (approximate answers acceptable).

Answer 1

Step-by-step explanation:

The formula for the work done on a spring is:

`W = (1)/(2)kx^(2)`

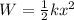
where k is the spring constant and x is the change in length of the string

For the first statement,

x = (a-1.1), W = 5

=>
`5 = (1)/(2)k(a-1.1)^(2)`

Now making k the subject of formula, we have:

`k = (10)/((a-1.1)^2) ---------------- (A)`

For the second statement,

x = (a-4.8), W = 9

=>
`9 = (1)/(2)k(a-4.8)^(2)`

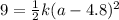
Now making k the subject of formula, we have:

`k = (18)/((a-4.8)^(2) ) ------------------------- (B)`

Equating A and B since k is constant, we have:

`(10)/((a-1.1)^(2) ) = (18)/((a-4.8)^(2) )`

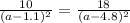
solving for the value of a

`8a^(2) +56.4a-208.62=0`

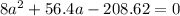
solving for a, we get:

a = 2.6801 or -9.7301

but since length cannot be negative, a = 2.68m

substituting the value of a in equation B, we have:

`k=(18)/((2.68-4.8)^(2) )`

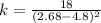
k = 4.005