Question

A California grower has an 80-acre farm on which to plant strawberries and tomatoes. The grower has available 600 hours of labor per week and 800 tons of fertilizer, and he has contracted for shipping space for a maximum of 60 acres’ worth of strawberries and 50 acres’ worth of tomatoes. An acre of strawberries requires 8 hours of labor and 5 tons of fertilizer, whereas an acre of tomatoes requires 4 hours of labor and 20 tons of fertilizer. The profit from an acre of strawberries is $500, and the profit from an acre of tomatoes is $300. The farmer wants to know the number of acres of strawberries and tomatoes to plant to maximize profit.

a. Formulate a linear programming model for this problem.
b. Graphically illustrate the feasible area and identify all the possible extreme points.
c. Solve the model – find the optimal solution points and the optimal objective function value.

Answer 1

a)

P=500s+300t

`s+t \leq 80`

`s\leq 60`

`T \leq 50`

`8s+4t \leq 600`

`5s+20t \leq 800`

`s \geq 0`

`t \geq 0`

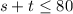
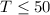
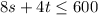
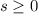
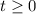
b) See attached picture.

Possible extreme points:

(0,0), (0,40), (160/3, 80/3), (60,20), (60,0)

c) Optimal solution points:

(0,0), (0,40), (160/3, 80/3), (60,20), (60,0)

Optimal objective function value happens at (60,20) for a profit of $36,000.

Step-by-step Explanation:

a) In order to find the linear programming model, we need to start by setting our variables up.

s= number of acres of strawberries to plant.

t = number of acres of tomatos to plant.

With this we can start by setting our ojective function up, which is the profit function.

"The profit from an acre of strawberries is $500, and the profit from an acre of tomatoes is $300."

Our objective function is:

P=500s+300t

Next, we need to set our restrictions up, which come from the rest of the sentences of the problem:

"A California grower has an 80-acre farm on which to plant strawberries and tomatoes." This tells us that we can plant as much as 80 acres of strawberries and tomatoes, so our first restriction is:

`s+t \leq 80`

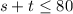
next:

"...and he has contracted for shipping space for a maximum of 60 acres’ worth of strawberries and 50 acres’ worth of tomatoes."

This sentence gives us the next two restrictions:

`s \leq 60`

`T \leq 50`

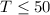
"The grower has available 600 hours of labor per week...", " An acre of strawberries requires 8 hours of labor..." and "...an acre of tomatoes requires 4 hours of labor...".

These sentences give us the next restriction:

`8s+4t \leq 600`

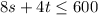
"The grower has available...800 tons of fertilizer...", "An acre of strawberries requires...5 tons of fertilizer", "...an acre of tomatoes requires...20 tons of fertilizer."

with this information we can build our next restriction:

`5s+20t \leq 800`

and finally, we also know that we cannot plant less than 0 acres of tomatos or strawberries since that would become a loss. So the final restrictions are:

`s \geq 0`

`t \geq 0`

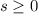
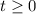
So the linear programmin model is the following:

P=500s+300t

`s+t \leq 80`

`s \leq 60`

`T \leq 50`

`8s+4t \leq 600`

`5s+20t \leq 800`

`s \geq 0`

`t \geq 0`

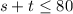
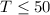
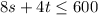
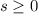
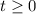
b) Once we have the linear programming model, we can go ahead and graph each of the restrictions. All the restrictions are graphed the same so I will give a brief explanation on how to graph the first one.

So let's take the first restriction:

`s+t \leq 80`

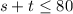
we can start by turning it into an equation:

s+t=80

and pick any value we wish for s. We can pick s=0 since that will simplify the work:

0+t=80

therefore t=80

the first point to plot is (0,80)

in order to find the second point to plot we can set t=0 so we get:

s+0=80

s=80

therefore the second point to plot is (80,0)

We can plot these two points on our coordinate axis and connect them with a solid line.

Next, we know that the region to shade should be less than or equal to 80, so we pick a test point above and below the graph. Let's pick (100,60) and (0,0)

for (100,60) we get that:

`100+60 \leq 80`

`160 \leq 80`

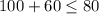
this is false so that region should not be shaded. Let's take the other test point:

for (0,0) we get:

`0+0\leq 80`

`0 \leq 80`

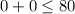
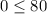
is true, so we should shade the region below the graph.

The same procedure is done with the rest of the restrictions and we have as a result the graph in the attached picture.

The feasible area is the area all the shaded areas have in common.

The extreme points are the vertices of the polygon formed by the feasible area, we can find them graphically or algebraically.

If we were to find them algebraically we would solve the corresponding system of equations. The first point (0,0) is found at the intersection of the restrictions:
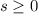`s \geq 0` and
`t \geq 0`.

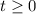The second extreme point is at the intersection of the restrictions:
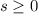`s \geq 0` and
`5s+20t \leq 800`, which yields (0,40).

The next extreme point is at the intersection of the restrictions:
`5s+20t \leq 800` and
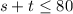`s+t \leq 80`. When solving this system of equations we get the point: (160/3, 80/3).

The next extreme point is at the intersection of the restrictions:
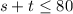`s+t \leq 80` and
`s \leq 60` which yields (60,20)

and the final extreme point is at the intersection of the restriction:
`s \leq 60` and
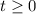`t \geq 0` which yields (60,0)

so the possible extreme points are: (0,0), (0,40), (160/3, 80/3), (60,20), (60,0).

c) Now we solve the model, in order to solve the model we need to use the optimal solution points and evaluate them in the objective function:

P=500s+300t.

See attached table for the results of substituting the optimal points.

So the optimal point will happen at (60,20) with a profit of $36,000.