Question

The concentration, C, in ng/ml, of a drug in the blood as a function of the time, t, in hours since the drug was administered is given by C = 15te−0.2t. The area under the concentration curve is a measure of the overall effect of the drug on the body, called the bioavailability. Find the bioavailability of the drug between t =0 and t =3

Answer 1

`\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 45.713 \ \text{ng/mL}`

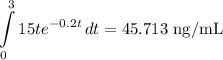
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Integration

• Integrals

Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

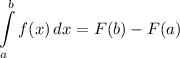
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

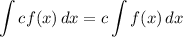
U-Substitution

Integration by Parts:
`\displaystyle \int {u} \, dv = uv - \int {v} \, du`

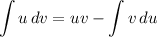
• [IBP] LIPET: Logs, inverses, Polynomials, Exponentials, Trig

Area of a Region Formula:
`\displaystyle A = \int\limits^b_a {[f(x) - g(x)]} \, dx`

Explanation:

*Note:

It is given that the area under the concentration curve is equal to the bioavailability.

Step 1: Define

Identify

`\displaystyle C = 15te^(-0.2t) \\\left[ 0 ,\ 3 \right]`

Step 2: Integrate Pt. 1

1. Substitute in variables [Area of a Region Formula]:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt`
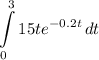
2. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 15 \int\limits^3_0 {te^(-0.2t)} \, dt`

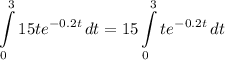
Step 3: Integrate Pt. 2

Identify variables for integration by parts using LIPET.

1. Set u:
   `\displaystyle u = t`
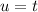
2. [u] Differentiate [Basic Power Rule]:
   `\displaystyle du = dt`
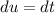
3. Set dv:
   `\displaystyle dv = e^(-0.2t) \ dt`
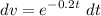
4. [dv] Exponential Integration [U-Substitution]:
   `\displaystyle v = (-e^(-0.2t))/(0.2)`

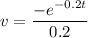
Step 4: Integrate Pt. 3

1. [Integral] Integration by Parts:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 15 \Bigg[ (-te^(-0.2t))/(0.2) \bigg| \limits^3_0 - \int\limits^3_0 {(-e^(-0.2t))/(0.2)} \, dt \Bigg]`
2. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 15 \Bigg[ (-te^(-0.2t))/(0.2) \bigg| \limits^3_0 + (1)/(0.2) \int\limits^3_0 {e^(-0.2t)} \, dt \Bigg]`

Step 5: Integrate Pt. 4

Identify variables for u-substitution.

1. Set u:
   `\displaystyle u = -0.2t`
2. [u] Differentiation [Basic Power Rule, Multiplied Constant]:
   `\displaystyle du = -0.2 \ dt`
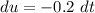
3. [Limits] Switch:
   `\displaystyle \left \{ {{t = 3 ,\ u = -0.2(3) = -0.6} \atop {t = 0 ,\ u = -0.2(0) = 0}} \right.`

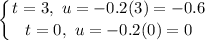
Step 6: Integrate Pt. 5

1. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 15 \Bigg[ (-te^(-0.2t))/(0.2) \bigg| \limits^3_0 - (1)/(0.04) \int\limits^3_0 {-0.2e^(-0.2t)} \, dt \Bigg]`
2. [Integral] U-Substitution:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 15 \Bigg[ (-te^(-0.2t))/(0.2) \bigg| \limits^3_0 - (1)/(0.04) \int\limits^(-0.6)_0 {e^(u)} \, du \Bigg]`
3. [Integral] Exponential Integration:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 15 \Bigg[ (-te^(-0.2t))/(0.2) \bigg| \limits^3_0 - (1)/(0.04)(e^u) \bigg| \limits^(-0.6)_0 \Bigg]`
4. Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 15 \Bigg[ -8.23217 - (1)/(0.04)(-0.451188) \Bigg]`
5. Simplify:
   `\displaystyle \int\limits^3_0 {15te^(-0.2t)} \, dt = 45.713`

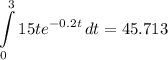
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration