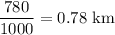Question

In reaching her destination, a backpacker walks with an average velocity of 1.32 m/s, due west. This average velocity results, because she hikes for 6.77 km with an average velocity of 2.01 m/s due west, turns around, and hikes with an average velocity of 0.667 m/s due east. How far east did she walk (in kilometers)

Answer 1

0.78 km

Step-by-step explanation:

The average velocity for the whole journey is given total displacement ÷ total time.

She traveled west first, then east later. Since the average velocity is towards the the west, then the total displacement is toward the west. This informs us she traveled a farther distance toward the west than the east.

Let
`t_1` be the time for the first journey west and
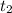`t_2` the time for the eastward journey.

From velocity = displacement ÷ time,

Time = displacement ÷ velocity

`t_1=(6770)/(2.01)=3368`

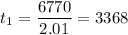
Let
`d` be the displacement east. Then

`(d)/(t_2)=0.667`

`t_2=(d)/(0.667)=1.5d`

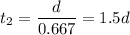
For the whole journey,

`(6770-d)/(t_1+t_2)= 1.32`

`(6770-d)/(3368+t_2)= 1.32`

`6670-d = 1.32(3368+t_2)`

`6670-d = 4446+1.32t_2`

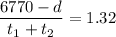
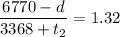
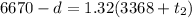
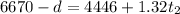
But
`t_2=1.5d`

`6670-d = 4446+1.32*1.5d`

`6670-d = 4446+1.98d`

`6670-4446 = d+1.98d`

`2324 = 2.98d`

`d=(2324)/(2.98)= 780`

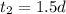
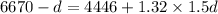
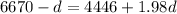
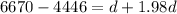
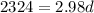
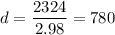
In km, this
`(780)/(1000)=0.78 \text{ km}`