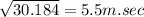Question

What minimum speed does a 200 g puck need to make it to the top of a frictionless ramp that is 4.1 m long and inclined at 22 ∘?

Answer 1

5.5 m/ sec

Step-by-step explanation:

Because the inclined surface is frictionless so we can assume that total change of energy is zero

i-e ΔE = 0

Or we can say that difference between final and initial energy is zero i-e

Ef- Ei =0

Where,

Ef= final energy at the top of the ramp= KEf+PEf

Ei= Initial energy at the bottom of the ramp=KEi+PEi

So we have

(KEf+PEf)-(KEi+PEi)=0

==>KEf-KEi+PEf-PEi=0 -------------(1)

KEf = mgh = 200×9.8×h

Where h= Sin 22 = h/d= h/4.1

or

0.375×4.1=h

or h= 1.54 m

So, PEf= 200×9.8×1.54=3018.4 j

and KEf= 1/2 m
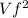`Vf^(2)`= 0.5×200×0=0 j

PEi= mgh = 200×9.8×0=0 j

KEi= 1/2 m
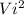`Vi^(2)`=0.5×200×
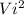`Vi^(2)`=100
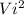`Vi^(2)` j

Put these values in eq 1, we get;

0-100
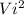`Vi^(2)`+3018.4-0=0

-100
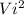`Vi^(2)`=-3018.4

==>
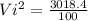`Vi^(2)= (3018.4)/(100)` = 30.184

==> Vi =
`√(30.184) = 5.5 m.sec`