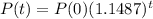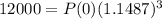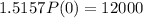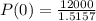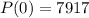Question

The population of a community is known to increase at a rate proportional to the number of people present at time t. The initial population P0 has doubled in 5 years. Suppose it is known that the population is 12,000 after 3 years. What was the initial population P0?

Answer 1

P(0) = 7,917

Explanation:

The population of the community is given by the following formula:

`P(t) = P(0)(1+r)^(t)`

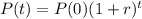
In which P(0) is the initial population and r is the growth rate.

The initial population P0 has doubled in 5 years.

This means that

`P(5) = 2P(0)`

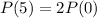
Which lets us find r.

`P(t) = P(0)(1+r)^(t)`

`2P(0) = P(0)(1+r)^(5)`

`(1+r)^(5) = 2`

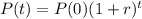
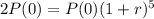
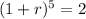
Applying the 5th root to both sides

`1+r = 1.1487`

`r = 0.1487`

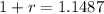
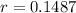
So

`P(t) = P(0)(1.1487)^(t)`

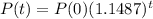
Suppose it is known that the population is 12,000 after 3 years.

With this, we find P(0)

`P(t) = P(0)(1.1487)^(t)`

`12000 = P(0)(1.1487)^(3)`

`1.5157P(0) = 12000`

`P(0) = (12000)/(1.5157)`

`P(0) = 7917`