Question

The protein catalase catalyzes the reaction The Malcolm Baldrige National Quality Award aims to:

2H2O2 (aq) ⟶ 2H2O (l) + O2 (g) and has a Michaelis–Menten constant of K M = 25 mM and a turnover number of 4.0 × 10 7 s − 1. The total enzyme concentration is 0.012 μM and the initial substrate concentration is 5.14 μM. Catalase has a single active site. Calculate the value of R max (often written as V max ) for this enzyme.

Answer 1

The question is missing a part, so the complete question is as follows:

The protein catalase catalyzes the reaction The Malcolm Bladrigde National Quality Awards aims to: 2H2O2 (aq) ⟶ 2H2O (l) + O2 (g) and has a Michaelis-Menten constant of KM = 25mM and a turnover number of 4.0 × 10 7 s -1. The total enzyme concentration is 0.012 μM and the intial substrate concentration is 5.14 μM. Catalase has a single active site. Calculate the value of Rmax (often written as Vmax) for this enzyme. Calculate the initial rate, R (often written as V0), of this reaction.

1) Calculate Rmax

The turnover number (Kcat) is a ratio of how many molecules of substrate can be converted into product per catalytic site of a given concentration of enzyme per unit of time:

Kcat =
`(Vmax)/(Et)`,

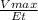where:

Vmax is maximum rate of reaction when all the enzyme sites are saturated with substrate

Et is total enzyme concentration or concentration of total enzyme catalytic sites.

Calculating:

Kcat =
`(Vmax)/(Et)`

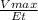
Vmax = Kcat · Et

Vmax = 4×
`10^(7)` · 1.2 ×
`10^(-8)`

Vmax = 4.8 ×
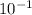`10^(-1)` M

2) Calculate the initial rate of this reaction (R):

The Michaelis-Menten equation studies the dynamics of an enzymatic reaction. This model can explain how an enzyme enhances the rate of a reaction and how the reaction rate depends on the concentration of the enzyme and its substrate. The equation is:

V0 =
`([S].(Vmax))/(KM + [S])`, where:

[S] is the substrate's concentration

KM is the Michaelis-Menten constant

Substituting [S] = 5.14 ×
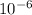`10^(-6)`, KM = 2.5 ×
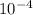`10^(-4)` and Vmax = 4.8 ×
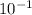`10^(-1)`, the result is V0 = 0.478 M.

The answers are Vmax = 4.8 ×
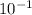`10^(-1)` M and V0 = 0.478 M.