Answer:
Step 1. Between 688 and 1016mm. Step 2. Less than 688mm.
Explanation:
The 68-95-99.7 rule roughly states that in a normal distribution 68%, 95% and 99.7% of the values lie within one, two and three standard deviation(s) around the mean. The z-scores represent values from the mean in a standard normal distribution, and they are transformed values from which we can obtain any probability for any normal distribution. This transformation is as follows:
 (1)
(1)

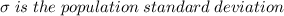
And x is any value which can be transformed to a z-value.
Then, z = 1 and z = -1 represent values for one standard deviation above and below the mean, respectively; values of z = 2 and z =-2, represent values for two standard deviations above and below the mean, respectively and so on.
Because of the 68-95-99.7 rule, we know that approximately 95% of the values for a normal distribution lie between z = -2 and z = 2, that is, two standard deviations below and above the mean as remarked before.
Step 1: Between what values do the monsoon rains fall in 95% of all years?
Having all this information above and using equation (1):

For z = -2:
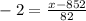
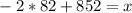
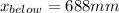
For z = 2:

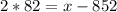
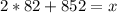
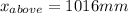
Thus, the values for the monsoon rains fall between 688mm and 1016mm for approximately 95% of all years.
Step 2: How small are the monsoon rains in the driest 2.5% of all years?
The driest of all years means those with small monsoon rains compare to those with high values for precipitations. The smallest values are below the mean and at the left part of the normal distribution.
As you can see, in the previous question we found that about 95% of the values are between 688mm and 1016mm. The rest of the values represent 5% of the total area of the normal distribution. But, since the normal distribution is symmetrical, one half of the 5% (2.5%) of the remaining values are below the mean, and the other half of the 5% (2.5%) of the remaining values are above the mean. Those represent the smallest 2.5% and the greatest 2.5% values for the normally distributed data corresponding to the monsoon rains.
As a consequence, the value x for the smallest 2.5% of the data is precisely the same at z = -2 (a distance of two standard deviations from the mean), since the symmetry of the normal distribution permits that from the remaining 5%, half of them lie below the mean and the other half above the mean (as we explained in the previous paragraph). We already know that this value is x = 688mm and the smallest monsoons rains of all year are less than this value of x = 688mm, representing the smallest 2.5% of values of the normally distributed data.
The graph below shows these values. The shaded area are 95% of the values, and below 688mm lie the 2.5% of the smallest values.