Answer:
a) 4.33 pC b) 5.44*10² N/C
Step-by-step explanation:
a) The vertical deflecting plates of an oscilloscope form a parallel-plate capacitor.
The value of the capacitance, for a parallel-plate capacitor with air dielectric, can be found to be as follows, applying Gauss' law to the surface of one of the plates, and assuming a uniform surface charge density:
C = ε₀*A / d
where ε₀ = 8.85*10⁻¹² F/m, A = (0.03m)², and d = 0.046 m (we assume that the informed value of 4.6 m is a typo, as no oscilloscope exists with this separation between plates).
Replacing by these values, we find the equivalent capacitance of the plates, as follows:
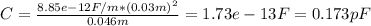
By definition, the capacitance of any capacitor can be expressed as follows:

where Q= charge on any of the plates, and V= potential difference between them.
As we know C and V, we can find Q as follows:
Q = C*V = 0.173*10⁻¹² F * 25.0 V = 4.33*10⁻¹² C = 4.33 pC
b) We can find the electric field in several ways, but one very easy is applying Gauss' Law to a pillbox with a face outside one of the plates (paralllel to it) and the other inside the surface.
The total electric flux through the surface must be equal to the enclosed charge, divided by ε₀.
If we look to the flux crossin any face, we find that the only one that has a non-zero flux, is the one outside the surface.
As the electric crossing the boundary must be normal to the surface (in electrostatic conditions, no tangential field can exist on the surface) , and we assume that the surface charge density that creates it is constant across the surface, we can write the Gauss ' Law as follows:
E*A = Q / ε₀
where A = area of the plate = (.03m)² = 9*10⁻⁴ m², Q= charge on one of the plates = 4.33*10⁻¹² C (as we found in a)) and ε₀ = 8.85*10⁻¹² N/C.
Replacing by these values, and solving for E, we have:
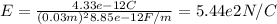
⇒ E = 5.44*10² N/C