Solution:
x = 10sin 2t + 15cos 2t +100
v = dx/dy = 20cos 2t - 30sin 2t
a = dv/dt = 40sin 2t - 60cos 2t
For trigonometric function set calculator to radian:
(a) At t = 1 s x1 = 10sin 2 + 15cos 2 + 100 = 102.9
v1 = 20cos 2 - 30sin 2 = -35.6
a1 = -40sin 2 - 60cos 2 = -11.40
(b) Maximum velocity occure when a = 0.
-40sin 2t - 60cos 2t = 0
tan 2t = -60/40 = -1.5
2t = tan⁻¹ (-1.5) = -0.9828 and -0.9828 +

Reject the negative value. 2t = 2.1588
t = 1.0794

t = 1.0794
 for V
for V
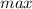
so
 =20cos(2.1588) -30sin(2.1588)
=20cos(2.1588) -30sin(2.1588)
= -36.056
Note that we could have also used
 =
=
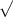 20² +30²
20² +30²
= 36.056
by combining the sine and cosine terms.
For
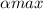 we can take the derivative and set equal to zero or just combine the sine and cosine terms.
we can take the derivative and set equal to zero or just combine the sine and cosine terms.
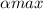 =
=
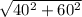
= 72.1 mm/
