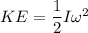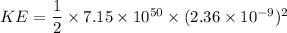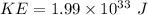Question

Uranus has a mass of 8.68 1025 kg and a radius of 2.56 107 m. Assume it is a uniform solid sphere. The distance of Uranus from the Sun is 2.87 1012 m. (Assume Uranus completes a single rotation in 17.3 hours and orbits the Sun once every 3.08 104 Earth days.)

(a) What is the rotational kinetic energy of Uranus on its axis?

_____________J

(b) What is the rotational kinetic energy of Uranus in its orbit around the Sun?

_____________J

Answer 1

Given,

Mass of the Uranus, M = 8.68 x 10²⁵ Kg

Radius of Uranus, R = 2.56 x 10⁷ m

Distance of Uranus, D = 2.87 x 10¹² days

a) Rotational Kinetic energy of the Uranus

moment of inertia of the Uranus

`I = (2)/(5)MR^2`

`I = (2)/(5)* 8.68* 10^(25)* (2.56* 10^7)^2`

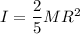
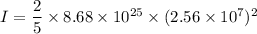
I = 22.75 x 10³⁹ kg.m²

Angular speed

`\omega = (2\pi)/(T) = (2\pi)/(17.3* 3600)`\

`\omega = 1 * 10^(-4)`

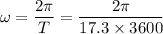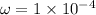
Rotational Kinetic energy

`KE = (1)/(2)I\omega^2`

`KE = (1)/(2)* 22.75* 10^(39)* (10^(-4))^2`

`KE = 11.38* 10^(31)\ J`

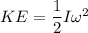
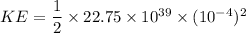
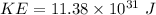
b) Rotational Kinetic energy of Uranus in its orbit around sun

moment of inertia of the Uranus

`I = (2)/(5)MR^2+ Ma^2`

`I = 22.75* 10^(39)+ 8.68* 10^(25)* (2.87* 10^(12))^2`

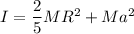
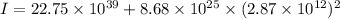
I = 7.15 x 10⁵⁰ kg.m²

Angular speed

`\omega = (2\pi)/(T) = (2\pi)/(3.08* 10^4* 3600* 24)`\

`\omega =2.36* 10^(-9)`

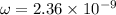
Rotational Kinetic energy

`KE = (1)/(2)I\omega^2`

`KE = (1)/(2)* 7.15* 10^(50)* (2.36* 10^(-9))^2`

`KE = 1.99* 10^(33)\ J`